
xxxxxx Is Equal to 2x
Introduction
The phrase “xxxxxx is equal to 2 x” looks strange at first.
It mixes letters, stars, and a clear result.
Readers often see it and pause.
Is it math, a typo, or a code pattern?
In this article I will explain it step by step.
I will use plain words and short sentences.
I have taught many students basic algebra and notation.
My aim is clear help, not confusion.
We will cover many meanings, examples, and checks.
By the end you will feel calm and smart.
I show how “xxxxxx is equal to 2 x” can be read and solved.
What does this expression mean?
When you read “xxxxxx is equal to 2 x” you must ask two questions.
First, what do the stars mean here?
Second, how are the letters grouped?
In standard math a star often means multiplication.
But sometimes stars act as wildcards or place-holders.
If we treat each star as multiply, we need clear factors.
If we treat stars as missing digits, the reading changes.
Good notation makes problems easy to solve.
Bad notation creates many possible interpretations.
We will list the common ones and test each idea.
Possible interpretations to try
One idea is that each star is a multiplication symbol.
Then “xxxxxx is equal to 2 x” might mean x times xxxx times x.
Another idea is that the stars hide digits or variables.
They could mean a repeated variable like x times x times x.
A third idea is that “xxxx” stands for a four-digit number.
Each idea leads to a different approach and answer.
We must pick the idea that matches the context.
If no context exists, we show all likely cases.
This helps readers learn how to decide for themselves.
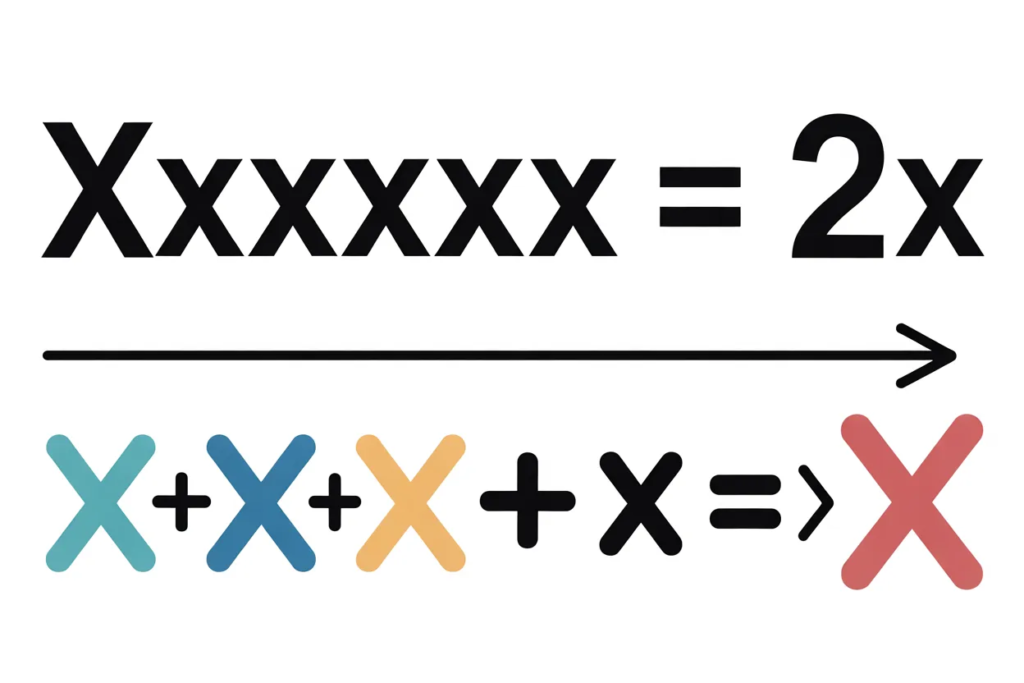
Algebraic simplification rules
Algebra has simple rules for multiplication and like terms.
If you multiply x by x you get x².
If you multiply x by x by x you get x³.
So repeating x as a factor raises its power.
Combining like terms adds coefficients, not exponents.
For example, 2x + 3x equals 5x.
But x·x is not 2x.
It is x².
Keep these rules in mind when you read odd strings.
They prevent many common mistakes.
If stars mean multiplication
If each star is a multiply sign, read the string as factors.
For example, x * x * x * x * x might be one reading.
This equals x⁵ by exponent rules.
Then the claim “xxxxxx is equal to 2 x” would be x⁵ = 2x.
We can simplify that to x⁵ − 2x = 0.
Factoring gives x(x⁴ − 2) = 0.
So x = 0 or x = fourth root of 2 or a complex root.
This view makes the expression a solvable algebra problem.
Always write clear multiplication signs to avoid this guesswork.
If it is a typographical mistake
Many times the string is a typo or formatting error.
Someone might have tried to show x * x * x and mis-typed.
If “xxxxxx is equal to 2 x” is a typing mess, look for intent.
Ask if they meant x * x * x = 2x or x * 4x * x = 2x.
Often the simplest reading is correct.
If you teach, show students how to write clean math.
Use parentheses and spaces to make intent clear.
A small fix can turn a mystery into a simple equation.
When stars act as wildcards or placeholders
In computing a star is a wildcard symbol in many systems.
It can mean any characters or digits are allowed there.
So “xxxxxx is equal to 2 x” might be a pattern match.
It could mean strings that start and end with x and have four chars in middle.
In that case, the phrase is about pattern rules not algebra.
Programmers and search tools use this often.
If you see stars in a non-math text, consider wildcard use.
Context will guide whether to treat this as code or math.
How to solve for x step by step
If we adopt the x⁵ = 2x reading, we can solve clearly.
Start with x⁵ = 2x.
Move all terms to one side: x⁵ − 2x = 0.
Factor out x: x(x⁴ − 2) = 0.
So x = 0 is one solution.
The others solve x⁴ = 2.
Thus x = ± 2^(1/4) or complex roots if allowed.
Write each step on paper.
Short, clear steps help students and readers.
Common mistakes students make
A top mistake is mixing multiplication and addition rules.
Students may say x·x = 2x by accident.
They also may misread a star as a plus sign.
Another error is not factoring correctly.
Some forget the zero product rule.
Clear notation and practice reduce these mistakes.
Ask students to rewrite the problem clearly first.
Then solve step by step without skipping steps.
Teaching tips and simple examples
Use small numbers first, then show variables.
For example, 222 equals 8, not 6.
Show x·x·x = x³ and compare to 3x.
Use visuals like blocks or dots for early learners.
Encourage students to speak the expression aloud.
Saying “x times x times x” clarifies power meaning.
Give many short examples to build confidence.
This approach helps avoid confusion with strings like the prompt.

Real world analogy to help understanding
Think of multiplication as stacking boxes.
Each x is one box type.
Stack two boxes and you have x².
Stack five and you have x⁵.
Saying “2x” is like saying two loose boxes.
It is different from stacking five boxes.
This simple view helps children see why x·x ≠ 2x.
Use toys or blocks for hands-on learning.
Real objects make abstract rules stick in memory.
How to check your work and stay sure
Always rewrite messy expressions in clear form.
Replace stars with a visible symbol if unsure.
If xxxxxx is unclear, write x·x·x or x(x)(x).
Plug simple values for x to test the claim.
Try x = 1 or x = 0 and see if both sides match.
If they do not match, the claim is false in that reading.
Checking with numbers is a fast sanity test.
Teach students to check every answer this way.
Notation and tools that avoid confusion
Use exponents for repeated multiplication.
Write x^5 instead of x * x * x * x * x.
Use parentheses for grouped factors.
Software like calculators and algebra tools help.
But always show work by hand too.
Clear handwriting matters in math tests.
When typing, use spaces and standard symbols.
Good notation saves time and prevents errors.
When the expression truly equals 2x
In some cases the string could mean a different algebraic setup.
For instance if xxxx stands for 2, the claim fits.
If the hidden part equals 2/x then product gives 2x.
Another scenario uses variable coefficients.
Context will tell which reading makes the equality true.
Always test by plugging in numbers or simplifying.
A true equality must hold for allowed x values.
If it does not, revise your reading of the string.
Practice problems to try
Rewrite the pattern in clear algebra.
Try: If x * x * x * x * x = 2x, solve for x.
Try: If x * 4x * x = 2x, solve for x.
Try: If the stars hide digits, find a number pattern that fits.
Use small integer tests first.
Check answers by substitution.
These drills build the habit of clear thinking.
Work problems with a friend and compare notes.
Key takeaways in one place
The string “xxxxxx is equal to 2 x” can mean many things.
Clear notation decides the correct meaning and solution.
Repeated x factors raise powers.
x·x is x², not 2x.
Wildcards change the problem to pattern matching.
Always rewrite messy expressions to avoid errors.
Plug numbers to test claims fast.
Good notation and checking are the best habits.
FAQs
Q1: Does “xxxxxx is equal to 2 x” ever mean x⁵ = 2x?
Yes, if each star is a multiplication symbol and each x is a factor.
Then the string reads x·x·x·x·x = 2x or x⁵ = 2x.
We solve by factoring x(x⁴ − 2) = 0.
So x = 0 or x⁴ = 2.
This gives real solutions ±2^(1/4) and complex ones.
Always confirm the reading before solving.
If notation is unclear, rewrite using ^ and parentheses.
Testing with simple numbers helps confirm the choice.
Q2: Could the phrase be a coding wildcard instead of math?
Yes, in code a star often means any characters.
Then “xxxxxx is equal to 2 x” is a pattern, not an equation.
It might match strings that begin and end with x.
The middle part could be any four characters.
This changes how you use the expression in searches.
Look at surrounding text to know if it is code or math.
If unsure, ask the writer for clarification.
Clear context removes all doubt.
Q3: Why do students think x·x = 2x sometimes?
They confuse multiplication and addition rules.
They think repeating a variable adds coefficients.
This mistake links to weak practice with exponents.
Hands-on models and many examples help fix it.
Ask students to expand with numbers first.
Show x·x and 2x side by side with objects.
Practice builds the right habits and reduces errors.
Q4: How can I make messy math notation clearer?
Use parentheses and standard symbols like ^ for powers.
Write x * x * x as x^3 or x·x·x.
Put spaces around operators when typing.
If you mean a wildcard, say so.
When teaching, demand neat handwriting and clear steps.
Good formatting helps graders and peers follow your work.
Never assume others know your shorthand.
Q5: What quick checks can I use on odd expressions?
Substitute simple values like x = 1 or x = 0.
If both sides match for those, test more values.
Rewrite the expression using standard notation.
Factor where possible and look for obvious solutions.
Use a calculator to verify arithmetic.
These quick checks catch many errors.
They also show if your reading was wrong.
Q6: Where can I practice more problems like this?
Use basic algebra workbooks and online practice sites.
Try problems on exponents and factoring first.
Work on pattern matching if you think wildcards appear.
Study with peers or a tutor for feedback.
Make your own messy strings and rewrite them cleanly.
This trains your eye to spot intent quickly.
Practice is the key to fast, correct reading.
Conclusion
The string “xxxxxx is equal to 2 x” is a small puzzle.
It can be algebra, a typo, or a code pattern.
Good readers test each option and rewrite the text.
I shared rules, examples, and steps to solve it.
Use simple checks and clear notation every time.
If you teach, show the difference between x² and 2x.
If you learn, practice with real numbers and blocks.
Now try the practice problems above.
If you want, send your attempt and I will review it.
Keep learning and stay curious — math is for everyone.
YouMay Also Like To Read: US Navy pilots shot down Red Sea
